Мы используем cookie для анализа и улучшения сайта. Продолжая пользоваться сайтом вы соглашаетесь с использованием cookie и нашей Политикой обработки персональных данных
Фата-моргана
Фата-моргана описана у Антона Павловича Чехова в повести «Чёрный монах». «Тысячу лет тому назад какой-то монах, одетый в чёрное, шел по пустыне, где-то в Сирии или Аравии… За несколько миль от того места, где он шёл, рыбаки видели другого чёрного монаха, который медленно двигался по поверхности озера. Этот второй монах был мираж. Теперь забудьте все законы оптики, которых легенда, кажется, не признаёт, и слушайте дальше. От миража получился другой мираж, потом от другого третий, так что образ чёрного монаха стал без конца передаваться из одного слоя атмосферы в другой.»
Фата-моргана – это редко встречающееся сложное оптическое явление в атмосфере, состоящее из нескольких форм миражей, при котором отдалённые объекты видны многократно и с разнообразными искажениями. Это явление часто водило за нос мореплавателей и не менее часто вдохновляло деятелей искусства. Так, в сказке Андерсена «Дикие лебеди» Элиза наблюдает это явление.
«Элиза опять устремила свой взор на замок, и вот горы, леса и замок сдвинулись вместе, и из них образовались двадцать одинаковых величественных церквей с колокольнями и стрельчатыми окнами».

Вы только посмотрите! Это 347-метровый лайнер вместимостью 4180 человек и водоизмещением 168 000 тонн. Который как ни в чём не бывало парит в воздухе!


Принцип Ферма. Закон преломления света.
При́нцип Ферма́ (принцип наименьшего времени Ферма) — постулат в геометрической оптике, согласно которому луч света между двумя точками распространяется по тому пути, который занимает меньше всего времени.


Кейс
Рассмотрим следующую задачу: представьте себе, что вы спасатель, и сидите в точке S, а в точке D тонет ЧЕЛОВЕК. Вы бегаете по земле быстрее, чем плаваете по воде.

Что делать спасателю, чтобы как можно скорее добраться до утопающего?


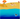
Конечно, в этих обстоятельствах спасателю глупо анализировать и вычислять, но маршрут, занимающий минимум времени, имеется и его можно рассчитать: это компромисс между прямой дорогой через точку J и дорогой, где меньше всего путь по воде, через точку N.
Найти: время, которое затратит спасатель на путь до тонущего человека, двигаясь по разным кривым.
После нахождения пути по кривым SJD и SND, выберите произвольно 2 точки на отрезке JN, так чтобы одна из них (точка L) была близко к N (например, LN = 5m), а другая точка (M) на расстоянии в 2 раза больше от N (MN=10m).
После нахождения пути по кривым SJD и SND, выберите произвольно 2 точки на отрезке JN, так чтобы одна из них (точка L) была близко к N (например, LN = 5m), а другая точка (M) на расстоянии в 2 раза больше от N (MN=10m).
⮛ Средний уровень
Свет из точки А падает на плоскую границу раздела двух сред и преломляется, попадая затем в точку В. Если скорости света в первой (верхней) и второй (нижней) средах различны (для определенности будем считать, что v₁>v₂), то ясно, что путь по прямой АВ требует совсем не минимального времени. Время будет меньшим, если свет проходит несколько больший путь в первой среде, где он распространяется с большей скоростью, но зато несколько меньший путь во второй среде.
Вывод из принципа Ферма.
Предположим, что свет затрачивает наименьшее время, если его путь проходит через точку С. Тогда любой другой путь левее или правее точки С займет большее время. Произвольную траекторию луча AFB можно задать с помощью переменной х - расстояния между точкой С и точкой F на границе раздела сред. Кривая зависимости времени распространения света от х должна иметь минимум в точке С, т. е. при х = 0 (см. рис).
Вблизи минимума время очень мало меняется с изменением х. Приближенно
при очень малых х это время вообще можно считать постоянным: на очень малом отрезке вблизи х = 0 кривую можно заменить маленьким отрезком прямой, параллельной оси х.
Вблизи минимума время очень мало меняется с изменением х. Приближенно
при очень малых х это время вообще можно считать постоянным: на очень малом отрезке вблизи х = 0 кривую можно заменить маленьким отрезком прямой, параллельной оси х.
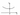
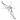
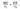
Сравним время распространения света на пути АСВ и на
пути AFB, считая, что x = FC очень мало. Проведем FM⟂AC
и CN⟂FB . На пути АСВ свет в первой среде проходит дополнительный путь МС (так как FC очень мало, то AF ≈ AM). Во второй среде дополнительный путь FN проходит уже луч, распространяющийся по траектории AFB. Так как время распространения света от точки А к точке В при малых значениях х должно быть постоянным, то время прохождения светом пути МС и пути FN должно быть одинаковым, т. е.:
пути AFB, считая, что x = FC очень мало. Проведем FM⟂AC
и CN⟂FB . На пути АСВ свет в первой среде проходит дополнительный путь МС (так как FC очень мало, то AF ≈ AM). Во второй среде дополнительный путь FN проходит уже луч, распространяющийся по траектории AFB. Так как время распространения света от точки А к точке В при малых значениях х должно быть постоянным, то время прохождения светом пути МС и пути FN должно быть одинаковым, т. е.:
Угол CFM равен углу падения α, а угол FCN - углу преломления β (так как x мало, то ∠NCB ≈ 90°). Поэтому МС = x*sinα и FN = x*sinβ. Подставляя эти выражения в предыдущее равенство, получим:

Показатель преломления n=c/V, значит отношение скоростей v₁/v₂ = n₂/n₁, отсюда получаем окончательное выражение для закона преломления:
sinα/sinβ = n₂/n₁
sinα/sinβ = n₂/n₁
⮛ Повышенный уровень

Прежде чем найти эту точку, давайте установим связь между поиском экстремума функции и принципом Ферма.
Принцип Ферма(принцип наименьшего времени Ферма) является примером так называемого принципа экстремума, который гласит, что любая система стремится к состоянию, при котором значение исследуемой величины принимает максимально или минимально возможное (т. н. экстремальное) значение.
В интересующем нас случае система состоит из источника света, луча, стеклянной пластины и точки внутри стекла, в которую попадает луч после преломления.
Задачей поиска экстремума в математике называют поиск минимума или максимума функции. Чтобы найти экстремумы (максимумы и минимумы) функции, нужно взять производную этой функции и приравнять её к нулю.
Нетрудно провести аналогию с задачей выше, в которой в качестве источника света выступает начальное местоположение спасателя, луч – сам спасатель (ЭТО ПУТЬ СПАСАТЕЛЯ).
Напомним, согласно Ферма, луч света между двумя точками распространяется по пути, который занимает меньше всего времени. Меньше всего времени - экстремальное значение исследуемой величины - времени! А нахождение экстремального значения функции – задача поиска экстремума. Теперь можно приступить к поиску точки на границе раздела воздуха и стекла, в которую должен упасть луч света, чтобы время его пути от точки S в точку D было минимальным. (Правильно поставлена задача?)
Вывод через производные.
Луч от источника света S, расположенного в первой среде, идет до точки В, расположенной во второй среде. Скорость света в первой среде V₁, показатель преломления n₁, во второй среде скорость света V₂, показатель преломления n₂.
В каждой среде кратчайшим путем будут прямые SA и AB. Точку A охарактеризуем расстоянием x от перпендикуляра, опущенного из источника на границу раздела. Определим время, затраченное на прохождение пути SAB:
t = SA / V₁ + AB / V₂ = √(h₀² + x²)/V₁ + √(h² + (l-x)²)/V₂
Для нахождения минимума времени найдем производную от t по x и приравняем её к нулю:
dt/dx=(2x/2V₁√(h₀²+ x²)) - (2(l-x)/2V₁√(h² + (l-x)²)) = 0
Заметим, что sinα = x/√(h₀² + x²), sinβ = (l-x)/√(h² + (l-x)²). Поэтому из выражения выше следует sinα/V₁ -sinβ/V₂= 0.
Отсюда сразу следует sinα/sinβ = V₁/V₂. Учитывая, что показатель преломления n=c/V, значит отношение скоростей v₁/v₂ = n2/n₁, отсюда получаем окончательное выражение для закона преломления:
sinα/sinβ = n₂/n₁
t = SA / V₁ + AB / V₂ = √(h₀² + x²)/V₁ + √(h² + (l-x)²)/V₂
Для нахождения минимума времени найдем производную от t по x и приравняем её к нулю:
dt/dx=(2x/2V₁√(h₀²+ x²)) - (2(l-x)/2V₁√(h² + (l-x)²)) = 0
Заметим, что sinα = x/√(h₀² + x²), sinβ = (l-x)/√(h² + (l-x)²). Поэтому из выражения выше следует sinα/V₁ -sinβ/V₂= 0.
Отсюда сразу следует sinα/sinβ = V₁/V₂. Учитывая, что показатель преломления n=c/V, значит отношение скоростей v₁/v₂ = n2/n₁, отсюда получаем окончательное выражение для закона преломления:
sinα/sinβ = n₂/n₁
Преломление света

Опыты.
1. Наберите неполную раковину воды (или любую другую достаточно крупную емкость) и опустите в нее линейку под некоторым углом к вертикали, так как показано на рисунке. Обратите внимание на то, что линейка как будто то бы «искривилась» и ее длина визуально изменилась. Попробуйте объяснить наблюдаемые явления.

2. Для того чтобы проделать еще один опыт для изучения преломления вам потребуется раковина наполненная водой и монета. Положите монетку на дно раковины и посмотрите на нее сверху, вы будете видеть монетку без искажений. Начинайте двигать голову в сторону (как показано на рисунке). Вы будете продолжать видеть монету и после того, как линия, соединяющая ваши глаза и монету будет пересекать край раковины. Данное явление связано с тем, что вследствие преломления вы будете наблюдать не за самой монетой, а за ее изображением, находящимся немного ближе к поверхности воды (подумайте о том, насколько ближе).
Миражи.
Вернёмся к миражам и фата-моргане.
Мираж — оптическое явление в атмосфере: преломление потоков света на границе между резко различными по плотности и температуре слоями воздуха. Для наблюдателя такое явление заключается в том, что вместе с реально видимым отдаленным объектом (или участком неба) также видно и его отражение в атмосфере.
Опишем появление миража в пустыне.
Солнце сильно нагревает песок пустыни. Воздух над песком на некоторое время становится менее плотным, чем в верхних слоях. Поэтому световые лучи, падая под малыми углами на поверхность нагретого слоя воздуха, искривляются и направляются вверх (рис. 1). Наблюдателю кажется, что они отражаются от земли. Обычно отражение происходит от поверхности воды. Поэтому и кажется, что между наблюдателем и горизонтом находится озеро. Образование мнимого изображения предметов из-за отражения света от слоев воздуха малой плотности называется миражом. В жаркий день можно часто наблюдать мираж на асфальтированных дорогах. Свет отражается от нагретых слоев воздуха, и создается впечатление луж, разлитых на асфальте (нижний мираж).
Иногда мираж можно наблюдать над холодной поверхностью моря (рис. 2), когда температура нижних слоев воздуха быстро растет с удалением от морской поверхности. В этом случае лучи света искривляются, поднимаясь в верхние, более теплые слои атмосферы (верхний мираж).


рис.1
рис.2
Фата-моргана – явление более сложное. Фата-моргана возникает в тех случаях, когда в нижних слоях атмосферы образуется (обычно вследствие разницы температур) несколько чередующихся слоев воздуха различной плотности, способных давать зеркальные отражения. В результате отражения, а также и преломления лучей, реально существующие (в том числе находящиеся далеко за горизонтом) объекты дают на горизонте или над ним по нескольку искаженных изображений, частично накладывающихся друг на друга и быстро меняющихся во времени, что и создаёт причудливую картину фата-морганы. В каждом отдельном случае фата-моргана своя.
Вот так выглядит, например, двойной мираж:

Фата-моргана может состоять из 3-х, 4-х и большего количества изображений, создавая порой целые города и причудливые конструкции.
Как преломление света встречается в повседневной жизни, кейсы.
Местоположение тел в воде. Преломление в воде.
Блеск бриллиантов. Мокрые предметы становятся темнее.
Местоположение тел в воде. Преломление в воде.
Блеск бриллиантов. Мокрые предметы становятся темнее.
Из-за явления преломления света, предметы находящиеся под водой мы видим искаженными. Расстояние до предметов под водой нам кажется не таким, какое оно в действительности. Неопытные купальщики нередко подвергаются большой опасности только потому, что забывают об одном любопытном следствии закона преломления света: они не знают, что преломление словно поднимает все погруженные в воду предметы выше истинного их положения. Дно пруда, речки, каждого водоема представляется глазу приподнятым почти на третью часть глубины; полагаясь на эту обманчивую мель, люди нередко попадают в опасное положение.
Вода и человек

Задача 1
Пловец, нырнувший с открытыми глазами, рассматривает из-под воды светящийся фонарик, находящийся над его головой на высоте h = 75 см над поверхностью воды. Какова видимая высота Н предмета над поверхностью воды? Показатель преломления воды n=4/3
Задача 2
Человек с лодки рассматривает дно. Как зависит кажущаяся глубина водоема h от угла α, образуемого лучом зрения с вертикалью? Действительная глубина водоема всюду одинакова и равна H.
Идеальные камни, в которых отсутствуют примеси, являются полностью прозрачными и имеют очень высокие показатели преломления алмазом света. Они отлично преломляют свет, разделяя его на все цвета радуги, что очень ценится в ювелирном производстве. Норма коэффициента преломления алмаза составляет от 2,417 до 2,421 (значительно больше, чем у воды или стекла).
Чем больше преломляется угол света, тем лучше блестит и играет цветами бриллиант.
Чем больше преломляется угол света, тем лучше блестит и играет цветами бриллиант.
Блеск бриллиантов
Про мокрые предметы, которые становятся темнее:



Дисперсия выражается в способности камня разлагать белый луч света на спектральные составляющие (лучи разных цветов). Это свойство постоянно для каждого вещества и определяется различной величиной показателя преломления для лучей разных цветов.
Величина дисперсии для алмаза равна 0,044, и это также одно из самых высоких значений среди минералов. Для того, чтобы дисперсия луча была заметна глазу, нужно, чтобы часть лучей после разложения на спектр вышла из камня наружу, а часть отразилась в бриллианте. Такое условие выполняется далеко не для всех лучей в бриллианте, поэтому большинство лучей, выходящих из него, белые, и только меньшая часть – цветные. Чем длиннее путь, который луч света проходит в бриллианте в результате многократных переотражений, тем больше расходятся цветные лучи и тем сильнее проявляется дисперсия. Как следствие, крупный бриллиант будет "играть" сильнее, чем мелкий. Сложная огранка алмазов позволяет увеличить угол расхождения лучей разных цветов.
Уникальное сочетание дисперсии, высокого коэффициента преломлением и твердостью алмаза, позволяющей отполировать его грани без малейших изъянов, позволило занять алмазу вершину в мире драгоценностей.
Задачи на вебинаре
Задача 1
Луч света падает на границу раздела двух сред под углом 30 градусов.
Показатель преломления первой среды 2,4. Определите показатель преломления второй среды, если известно, что отраженный от границы раздела луч и преломленный перпендикулярны друг другу.
Показатель преломления первой среды 2,4. Определите показатель преломления второй среды, если известно, что отраженный от границы раздела луч и преломленный перпендикулярны друг другу.
Задача 2
Водолаз определил угол преломления солнечных лучей в воде. Он
оказался равным 32° .На какой высоте над горизонтом находится Солнце?
оказался равным 32° .На какой высоте над горизонтом находится Солнце?
На дне ручья лежит камешек. Мальчик хочет в него попасть палкой.
Прицеливаясь, мальчик держит палку в воздухе под углом 45 градусов. На каком расстоянии от камешка палка воткнется в дно ручья, если его глубина 32 см?
Прицеливаясь, мальчик держит палку в воздухе под углом 45 градусов. На каком расстоянии от камешка палка воткнется в дно ручья, если его глубина 32 см?
Задача 3
Пловец, нырнувший с открытыми глазами, рассматривает из-под воды светящийся фонарик, находящийся над его головой на высоте h = 75 см над поверхностью воды. Какова видимая высота Н предмета над поверхностью воды? Показатель преломления воды
Задача 4
Человек с лодки рассматривает дно. Как зависит кажущаяся глубина водоема от угла , образуемого лучом зрения с вертикалью? Действительная глубина водоема всюду одинакова и равна.
Задача 5
Задача 6
Луч света падает на поверхность прозрачного стеклянного шара под углом α₀ =45° к радиусу, проведенному в точку падения.
Показатель преломления стекла, из которого изготовлен шар, n = 1.414. На какой угол отклонится луч от направления первоначального движения после выхода из шара? Ответ выразить в градусах.
Показатель преломления стекла, из которого изготовлен шар, n = 1.414. На какой угол отклонится луч от направления первоначального движения после выхода из шара? Ответ выразить в градусах.
Прямоугольная стеклянная пластинка толщиной 4 см имеет показатель преломления 1,6. На ее поверхность падает луч света под углом . Определите, на сколько сместится луч после выхода из пластинки в воздух.
Задача 7
Тонкий световой луч падает на боковую грань стеклянной призмы из воздуха под углом . Угол между боковыми гранями призмы равен . Показатель преломления воздуха равен 1, а стекла 1,41. Определите угол смещения луча от первоначального направления .
Задача 8
Задача 1
В дно пруда вертикально вбит шест высотой 1‚25 м. Определите длину тени на дне пруда, если солнечные лучи падают на поверхность воды под углом 38°, а шест целиком находится под водой.
Задача 2
Задача 3

В дно водоема глубиной 1,5 м вбита свая, которая выступает над поверхностью воды на 30 см. Найдите длину тени от сваи на дне водоема, если угол падения солнечных лучей равен 45°.
На горизонтальном дне водоема глубиной 1,2 м лежит плоское зеркало. На каком расстоянии от места вхождения лучей в воду этот луч снова выйдет на поверхность воды после отражения от зеркала? Угол падения луча равен 30° , показатель преломления воды 4/3.
Можно ли наблюдать полное внутреннее отражение при переходе света из воздуха в воду? Почему?
Задача 4
В жидкости с показателем преломления 1,8 помещен точечный источник света. На каком наибольшем расстоянии Н над источником надо поместить диск диаметром 4 см, чтобы свет не вышел из жидкости в воздух?
Задача 5
Луч света падает на границу раздела двух сред под углом .
Показатель преломления первой среды 2,4. Определите показатель преломления второй среды, если известно, что отраженный от границы раздела луч и преломленный перпендикулярны друг другу..
Показатель преломления первой среды 2,4. Определите показатель преломления второй среды, если известно, что отраженный от границы раздела луч и преломленный перпендикулярны друг другу..
Задача 6

Задача 1
Плоскопараллельная пластинка толщиной 5 см посеребрена с нижней стороны. Луч падает на верхнюю поверхность пластинки под углом 30°, частично отражается, а часть света проходит в пластинку, отражается от нижней ее поверхности и, преломляясь вторично, выходит в воздух параллельно первому отраженному лучу. Определите показатель преломления материала пластинки, если расстояние между двумя отраженными лучами 2,5 см.
Задача 2
Задача 3
Вблизи левого торца хорошо отполированной прозрачной пластины, показатель преломления которой n, расположен точечный источник света S (рис.). Толщина пластины H = 1 см, её длина L = 100 см. Свет от источника падает на левый торец пластины под всевозможными углами падения (0 — 90°). В глаз наблюдателя попадают как прямые лучи от источника, так и лучи, многократно испытавшие полное отражение на боковых гранях пластины. 1) Какое максимальное число отражений может испытать луч от источника, выходящий через правый торец пластины? Решите задачу для двух значений коэффициента преломления: n1 = 1,73, n2 = 1,3. 2) Укажите, в каком из этих двух случаев свет частично выходит из пластины через боковые грани.
Имеются две плоскопараллельные пластинки толщиной 16 и 24 мм, сложенные вплотную. Первая сделана из кронгласа с показателем преломления 1,5, а вторая – из флинтгласа с показателем преломления 1,8. На поверхность одной из них
падает луч света под углом 48° . Определите, на сколько сместится этот луч после выхода из пластинок в воздух. Зависит ли полученный результат от того, в какой
последовательности свет проходит пластинки? Порядок установки пластинок неважен: это показано на рисунке.
падает луч света под углом 48° . Определите, на сколько сместится этот луч после выхода из пластинок в воздух. Зависит ли полученный результат от того, в какой
последовательности свет проходит пластинки? Порядок установки пластинок неважен: это показано на рисунке.
Задача 4
Тонкий световой луч падает на боковую грань стеклянной призмы из воздуха под углом 45° . Угол между боковыми гранями призмы равен 30° . Показатель преломления воздуха равен 1, а стекла 1,41. Определите угол смещения луча от первоначального направления δ.
